Retour

Imprimer

fiche

Suivant

I LIMITE FINIE : 2

a ) LiMite finie en un point A.. 2

b ) Limite finie Pour f(x) en l'infinie pour x. 2

II LIMITE INFINIE. 3

a ) Limite en 0. 4

b ) limite en a. 4

c ) limite en l'infini 5

III REGLAGE ALGEBRIQUE. 5

a ) La somme. 5

b ) le produit 6

c ) le quotient 7

IV ASYMPTOTES. 8

a ) Asymptotes verticales. 8

b ) Asymptotes horizotaleS. 9

c ) Asymptotes obliques. 10

I LIMITE FINIE :

a ) LiMite finie en un point A

_{: Limite en 0}

Théorème: soit

Alors

Car +

Théorème: soit ont pour limite 0 en x = 0

_{: Limite finie en a ≠ 0}

Théorème: si P(x) est un polynôme alors

Exemple:

Théorème: si f est une fonction définie sur I et a Î I

alors

Exemple:

Déterminer la limite en -2

b ) Limite finie Pour f(x) en l'infini pour x

_{: Exemple}

x	10^1	10^2	10^3	10^4	10^10
	10^-1	10^-2	10^-3	10^-4	10^-10

Plus x devient "grand", plus devient "petit"

x	-10^1	-10^2	-10^3	-10^4	-10^10
	-10^1	-10^2	-10^3	-10^4	-10^10

Plus x devient "grand dans les négatifs", plus devient "petit"

Théorème:

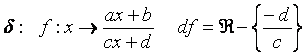
Théorème:

Théorème:

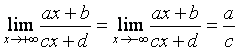
Calcule

Preuve:

or

II LIMITE INFINIE

a ) Limite en 0

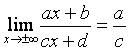
x	10^-1	10^-2	10^-3	10^-4	10^-10
	10^1	10^2	10^3	10^4	10^10

Quand x devient "très petit", devient "très grand".

x	-10^-1	-10^-2	-10^-3	-10^-4	-10^-10
	-10^1	-10^2	-10^3	-10^4	-10^10

Quand x deviens "très petit dans les négatif", deviens "très grand dans les négatif".

Théorème:

b ) limite en a

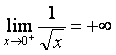
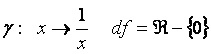
Théorème: soit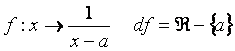

alors

Preuve:

c ) limite en l'infini

Théorème:

Exemple:

Théorème:

III REGLES ALGEBRIQUES

a ) La somme

Théorème: Soit f et g deux fonctions telles que

Exemple:

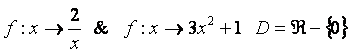
Détermine

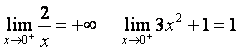
donc

Tableau de la somme

	L			+∞		-∞
	L'	-∞	+∞	+∞	-∞	-∞
	L+L'	-∞	+∞	+∞	?	-∞

Méthode pour lever la forme indéterminée [+∞+(-∞)]

Étape 1: factorises par le terme de plus haut degré et simplifier

Étape 2: chercher les limites de chaque facteur

Étape 3: conclusion

Déterminer :

Donc on a une forme indéterminée

or

donc

b ) le produit

Théorème: Soit f et g deux fonctions telles que et alors

Tableau des produits

	L	L ≠ 0		0		ou	-∞ +∞
	L'	ou	-∞ +∞	ou	-∞ +∞	ou	-∞ +∞
	LxL'	∞*		?		∞*

* on applique la règle des signes

Exemple: pour 0 x ∞

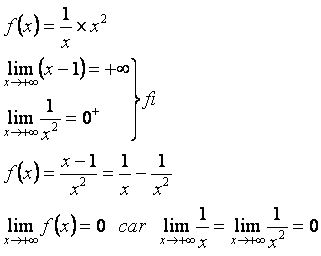
Méthode pour lever la forme indéterminée [0 ´ ∞]

Étape 1: développer le produit

Étape 2: effectuer les limites de chaque terme

Étape 3: conclusion

c ) le quotient

Théorème: Soit f et g définis sur I a Î I tell que alors

Tableau des produits

L	L ≠ 0		0		ou	-∞ +∞
L'	ou	-∞ +∞	ou	-∞ +∞	ou	-∞ +∞
LxL'	∞*		?		∞*

* on applique la règle des signes

f	L			+∞		0
g	L'	∞	0*	∞	0*	0	∞
		0*	∞*	?	∞*	?	0*

* on applique la règle des signes

Méthode pour lever la forme indéterminée

Étape 1: factoriser par le terme de plus haut degré

Étape 2: simplifier

Étape 3: chercher les limites de chaque élément

Étape 4: conclusion

Voir exercice 36

Méthode pour lever la forme indéterminée

Étape 1: factoriser "normalement"

Étape 2: simplifier

Étape 3: chercher les limites de chaque élément

Étape 4: conclusion

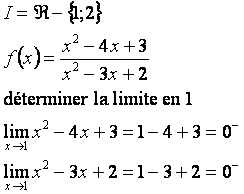
on a une forme indéterminée

Étape 1: on factorise

Factorisation de a

Pour x² – 4x + 3:

donc 2 racines réelles

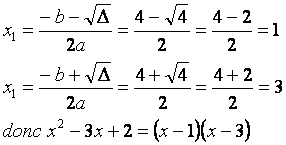
Pour x² – 4x + 3:

donc 2 racines réelles

IV ASYMPTOTES

a ) Asymptotes verticales

_{Définition – propriété:}

Soit a un réel et f une fonction; si alors la courbe C_f admet une asymptote verticale d'équation x = a

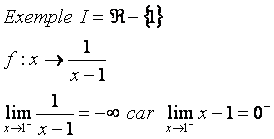
la courbe C_f admet donc une asymptote verticale d'équation x = 1

Remarque: on trouvera les asymptotes verticales que dans les valeurs interdites

b ) Asymptotes horizontaleS

_{Définition – propriété:}

Soit a un réel et f une fonction; si alors la courbe C_f admet une asymptote verticale d'équation

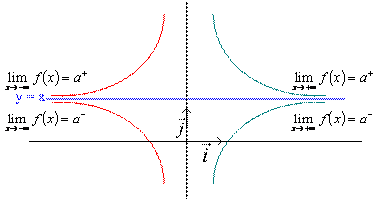
donc C_f admet une asymptote horizontale d'équation y = 1 en+ ¥ et en -¥

c ) Asymptotes obliques

_{Définition – propriété:}

Soit (D) une droite d'équation et C_f, la courbe d'une fonction f. Alors (D) une asymptote oblique a C_f, lorsque

Retour

Imprimer

fiche

Suivant