1 Le condensateur
| |
retour |
|
1.1 Définition
| |
retour |
Un condensateur est constitué de deux conducteurs dont les surfaces en regard
sont proches l'une de l'autre et séparées par un isolant. Les deux conducteurs
constituent les armatures du condensateur, l'isolant est son diélectrique.
Représentation d'un condensateur :

|
1.2 Propriétés
| |
retour |
Tension
de claquage d'un condensateur
C'est la plus petite tension qui provoque une étincelle entre les armatures
du condensateur.
Charge
et capacité d'un condensateur
On appelle charge du condensateur la charge de son armature positive.
La charge Q est liée à la tension U par :
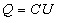
C désigne la capacité du condensateur. Elle dépend seulement de la forme
et des dimensions des armatures ainsi que de la nature du diélectrique.
La capacité d'un condensateur est une grandeur toujours positive.
La capacité d'un condensateur plan est donnée par la relation :
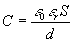
(er est appelée permittivité relative du milieu ) avec e0 la permittivité
du vide (e0 = 8, 84.10-12 S.I.), er la constante diélectrique qui dépend
de la nature du diélectrique placé entre les armatures (er = 1 pour
le vide et er 1 pour l'air), S la surface des armatures et d la distance
qui sépare les armatures. Dans le système SI, l'unité de capacité est
le Farad (F).
Energie
emmagasinée par un condensateur chargé
En choisissant d'orienter ainsi la portion de circuit :
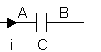
et en
appelant dq la variation de la charge de l'armature A pendant l'intervalle
de temps dt, on a toujours :
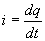
La loi d'Ohm pour un condensateur s'écrit :
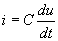
Un condensateur
chargé est un réservoir d'énergie. L'énergie emmagasinée par un condensateur
a pour expression :
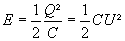
|
1.3 Réponse de l'association RC en série à un échelon de tension
| |
retour |
Un condensateur s’oppose aux brusques variations de tension
dans un circuit. Il n’y a pas de discontinuité de la tension aux
bornes d’un condensateur.
RC est la constante de temps d’un circuit comportant un générateur,
une résistance et un condensateur en série. RC s’exprime
en secondes dans le système SI.
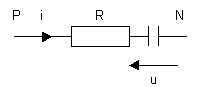
Equation caractéristique de la charge d’un condensateur
à travers la résistance R :
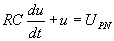
Equation caractéristique de la décharge d’un condensateur
à travers la résistance R :

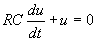
La tension aux bornes d’un condensateur pendant la charge
sous la tension constante UPN vérifie la relation :
 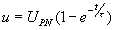
avec t = RC, la tension initiale aux bornes du condensateur
étant nulle.
La tension aux bornes d’un condensateur pendant la décharge
dans une résistance R vérifie la relation :
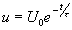
avec t = RC, U0 étant la tension initiale
aux bornes du condensateur.
|
2 Induction électromagnétique
| |
retour |
L’induction électromagnétique intervient :
- dans les générateurs électromagnétiques
- dans les alternateurs
- dans les dynamos
- dans les transformateurs
|
2.1 Courant induit et f.e.m. d'induction
| |
retour |
Tout circuit fixe fermé, placé dans un champ magnétique variable est le siège
d'un phénomène d'induction électromagnétique. La f.é.m. induite, encore
appelée f.é.m. d'induction, n'est pas localisée
|
2.2 Flux du champ B à travers l'induit
| |
retour |
Le flux F du champ uniforme
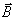 à travers le circuit plan d’aire S est défini par :
à travers le circuit plan d’aire S est défini par :
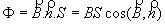 (la notion
de flux est hors-programme). (la notion
de flux est hors-programme).
Les effets de la f.é.m. d’induction tendent à
s’opposer à ceux du champ
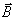 qui crée la f.é.m. d’induction.
qui crée la f.é.m. d’induction.
|
2.3 Loi de Lenz
| |
retour |
Enoncés de la loi de Lenz :
- La f.é.m. induite tend à s’opposer à toute variation
du flux inducteur.
- Le sens du courant induit est tel que le champ qu’il crée s’oppose
aux variations du champ inducteur.
- Le sens du courant induit est tel que ses effets produisent un flux qui s’oppose
toujours à la variation du flux inducteur qui en est la cause.
- Le courant induit crée un flux de signe opposé à celui
de la variation du flux inducteur.
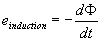 (
hors programme ) (
hors programme )
|
2.4 Réponse d'une association RL en série à un échelon de tension
| |
retour |
La constante de temps d’un circuit d’inductance L et de résistance
R est :

Variation de l’intensité lors de l’établissement
d’un régime permanent dans un circuit RL :
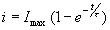
avec
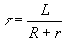 et et
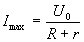
Variation de l’intensité durant la disparition du courant
dans le circuit :
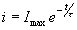
|
3 Phénomène d'auto-induction
| |
retour |
|
3.1 Flux propre à travers un circuit
| |
retour |
Un circuit parcouru par un courant électrique est plongé dans
son propre champ magnétique.
|
3.2 Auto-inductance d'un circuit
| |
retour |
L’inductance d’un circuit indéformable ne comportant pas
de substance ferromagnétique est telle que :
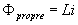 L est l’auto-inductance du
circuit L est l’auto-inductance du
circuit
La f.é.m. d’auto-induction a pour valeur :
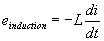 (
c’est la seule formule exigible ) (
c’est la seule formule exigible )
L’inductance d’un solénoïde
idéal de longueur l et de rayon r, comportant n
spires par unité de longueur est :
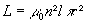 (
formule non exigible ) (
formule non exigible )
|
3.3 Aspect énergétique
| |
retour |
Loi d’Ohm pour une bobine :

Energie emmagasinée par une bobine parcourue par un
courant I :
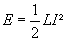
|