Lorsqu’on impose à la lumière de passer à travers des ouvertures (pupilles) de faible dimension (de l’ordre de quelques dixièmes de mm), le phénomène de diffraction se manifeste. Les lois usuelles de l’optique géométrique (principe de propagation rectiligne, lois de Descartes) tombent en défaut lorsqu’il y a diffraction.

Un faisceau parallèle tombant sur une ouverture circulaire (de diamètre a quelques dixièmes de mm), ménagée dans un plan opaque, ressort divergent. Il n’y a pas de propagation rectiligne : la pupille circulaire diffracte la lumière. On peut observer la tache de diffraction sur un écran éloigné : c’est le disque d’Airy.

Lorsqu’on s’affranchit de la diffraction, on est dans les conditions de l’optique géométrique. Les lois fondamentales de l’optique géométrique sont :

• le principe de propagation rectiligne,

• le principe du retour inverse,

• le principe d’indépendance des rayons lumineux,

• les lois de Descartes relatives à la réflexion et à la réfraction.

a) Le principe de propagation directe

Dans un milieu, homogène, isotrope, la lumière se propage en ligne droite.

b) Le principe de retour inverse

Le trajet d’un rayon lumineux à travers une suite de milieux transparents est indépendant du sens de propagation de la lumière.

La marche d’un rayon lumineux est indépendant de celle de ses voisins : ce principe très important est mis en œuvre pour la construction des images.

Les lois de Descartes s’énoncent ainsi : le rayon réfléchi appartient au plan d’incidence. Le rayon réfléchi est le symétrique du rayon incident par rapport à la normale au point d’incidence. Le rayon réfracté appartient aussi au plan d’incidence. Incident et réfracté sont de part et d’autre de la normale et l’on a la loi des sinus suivante :

avec et indice du milieu de propagation et angle par rapport à la normale pour la réflexion

et indice du milieu de propagation et angle par rapport à la normale pour la réfraction.

La lumière émise par une source est complexe. Analyser une lumière, c’est la décomposer en ses radiations constitutives. C’est obtenir son spectre. Les spectres sont obtenus à partir d’appareils appelés spectroscopes, dont l’élément fondamental est le système dispersif, prisme ou réseau. Les réseaux sont constitués d’un très grand nombre N de fentes parallèles, très serrées. Il y a interférence des N ondes issues des N fentes. Dans le cas des interférences à l’infini, les franges brillantes sont observées dans la direction q telle que :

( dans le cas d’une incidence perpendiculaire au réseau )

l est la longueur d’onde de la lumière et a’ représente le pas du réseau.

On distingue deux types de spectres d’émission : les spectres de raies et les spectres continus. Les spectres de raies sont caractéristiques des atomes émetteurs et les spectres continus dépendent peu de la nature du matériau constituant la source ; ils dépendent essentiellement de sa température.

L’ensemble des raies manquantes dans le spectre de la lumière transmise par une substance constitue le spectre d’absorption de la substance éclairée. Les spectres d’absorption et d’émission sont complémentaires : les raies d’émission et d’absorption apparaissent aux même longueurs d’ondes.

En 1900, Planck suppose que l’échange d’énergie entre matière et radiation électromagnétique se fait de manière discontinue. La valeur des grains ou quanta d’énergie est 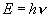avec h constante de Planck de valeur : 6, 62.10^-34 J.s. En 1905, Einstein introduit le modèle du photon pour décrire la lumière. Le photon est un corpuscule de masse nulle, de charge nulle, d’énergie, qui se déplace à la célérité de la lumière. Toute radiation peut être décrite comme une onde (modèle ondulatoire) ou comme une particule, le photon (modèle corpusculaire).

Pour Niels Bohr, en 1913, l’émission d’un photon d’énergi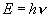e correspond à une diminution d’énergie de l’atome : son énergie passe d’une valeur supérieure 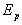à une valeur inférieure. On a ainsi :

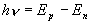ou

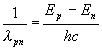
L’absorption d’un photon d’énergie 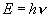correspond pour l’atome à un accroissement d’énergie de la valeur à la valeur. Seuls les photons dont l’énergie 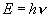est exactement égale à la valeur 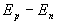peuvent être absorbés.

L’atome d’hydrogène est le plus simple qui soit : il est formé d’un proton (le noyau) et d’un électron. L’énergie de l’électron dans le champ du noyau est :

.

Cette énergie est appelée énergie de l’atome.

A toute particule en mouvement, on associe une onde et inversement. Dans le cas du photon, on a la relation :

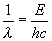
avec l longueur d’onde de l’onde associée et E énergie du photon.

La longueur d’onde est d’autant plus courte que l’énergie de la particule est grande.