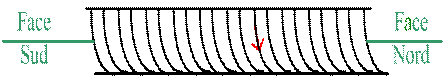|
1)
Les aimants permanents
2)
Les électro-aimants (bobines parcourues
par un courant)
3)
Le champ magnétique terrestre
On saupoudre de limaille de fer une plaque de verre
placée dans un champ magnétique.
Les lignes de champ magnétiques matérialisées
par la limaille de fer relient la région polaire Nord à la région polaire Sud
d'un aimant.
L'ensemble de ces lignes de champ constitue le
spectre magnétique.
 
PROPRIÉTÉS :
-
les lignes de champ ne se coupent pas.
-
Les lignes de champ sont des lignes
fermées.

a) origine : le point considéré M
b) direction : tangente au point M à la ligne champ
c) sens : c'est celui de la ligne de champ qui passe
par le point M c'est-à-dire le sens sud-nord d'une aiguille aimantée placée
en M.
d) norme : c'est l'intensité du champ au point M.
Elle est mesurée à l'aide d'un testa mètre placé au point M. Son unité est le
testa (T).
REMARQUES :
Champ
magnétique uniforme :
Entre les branches
d'un aimant en U, les lignes de champ sont parallèles et le vecteur champ
magnétique y est constant.
Pour caractériser le vecteur  , il faut déterminer : , il faut déterminer :
a)
sa direction :
perpendiculaire au plan de la bobine.
b)
Son sens : on emploi
l'une des deux méthodes suivantes : -
la règle du tire-bouchon de Maxwell : en tournant dans le sens de I, on
progresse dans le sens du vecteur  . .
-
la règle de la main droite : on place la main droite sur la bobine, les
doigts dans le sens de I, les lignes de champ sont orientées à l'intérieur du
solénoïde dans le sens du pouce.
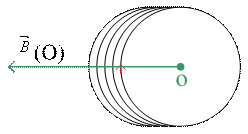 
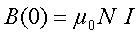
B(o)
= intensité du champ magnétique au centre du solénoïde
N = nombre de spires par mètre du
solénoïde
µ0 = perméabilité du vide. (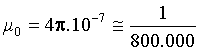 ) )
·
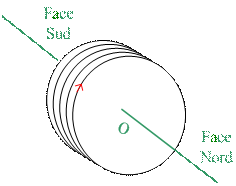
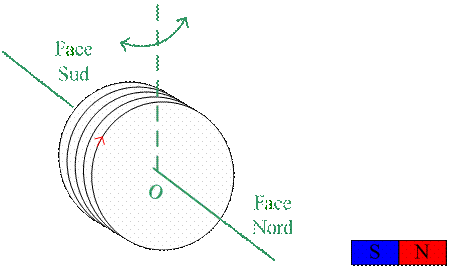
les lignes de champ entrent
dans la bobine par la face sud et en sortent par la face nord.
·
Règle du tire-bouchon : en
tournant dans le sens de I, on progresse dans le sens face sud – face nord de
la bobine.
·
Règle de la main droite :
on place la main droite sur la bobine, les doigts dans le sens de I, le pouce
indique le sens face sud / face nord de la bobine.
·
Une bobine parcourue par un
courant se comporte exactement comme un aimant dont le pôle sud serait sa
face sud et le pôle nord sa face nord.
·
2 pôles de même nom se
repoussent et 2 pôles de noms opposés s'attirent.
La force de Lorenz exercée sur la particule en
mouvement est :

F
en N
q
= charge de la particule en coulomb (C)
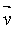 = vecteur vitesse de
la particule m-s-1 = vecteur vitesse de
la particule m-s-1
 = vecteur
champ magnétique (T) = vecteur
champ magnétique (T)
sin ( ) = sinus de l'angle entre les vecteurs ) = sinus de l'angle entre les vecteurs 
Expression arithmétique :
F
= |q| v B sin (q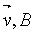 ) )
 est un vecteur de direction
perpendiculaire au plan défini par les vecteurs q est un vecteur de direction
perpendiculaire au plan défini par les vecteurs q 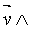 
Lorsque
les vecteurs  sont orthogonaux, la
direction et le sens du vecteur sont orthogonaux, la
direction et le sens du vecteur 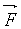 sont donnés par la règle
des 3 doigts de la main droite. sont donnés par la règle
des 3 doigts de la main droite.
 : pouce : pouce
 : index : index
 : majeur : majeur
L’
intensité du vecteur  sans sans
F = êqï v B
|

|
 : dans le 3 D, le 3éme axe ‘‘rentre dans la
feuille’’ : dans le 3 D, le 3éme axe ‘‘rentre dans la
feuille’’
|
|
 : dans le 3 D, le 3éme axe ‘‘sort de la feuille’’ : dans le 3 D, le 3éme axe ‘‘sort de la feuille’’
|
Lorsque les vecteurs 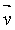 et et  sont colinéaires, (même
plan) la force de Lorenz sont colinéaires, (même
plan) la force de Lorenz vaut vaut 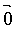 . .
La force de Laplace , vecteur 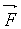 , exercée sur le conducteur est : , exercée sur le conducteur est :
I : Intensité dans le conducteur F = F l B sin (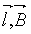 ) )
 vecteur porté par le
conducteur de même sens que l’ intensité positive, de norme égale à l, longueur
du conducteur soumise au champ magnétique. vecteur porté par le
conducteur de même sens que l’ intensité positive, de norme égale à l, longueur
du conducteur soumise au champ magnétique.
 vecteur champ
magnétique vecteur champ
magnétique
( ) angle entre les vecteurs ) angle entre les vecteurs  et et 
Lorsque le conducteur et la direction de sont perpendiculaires, la direction et le
sens de la force de Laplace 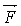 sont donnez par la
règle des 3 doigts la main droite. sont donnez par la
règle des 3 doigts la main droite.
 pouce pouce
index
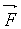 majeur majeur
L’intensité de 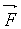 vaut vaut
REMARQUE 1
: Lorsque les vecteurs I 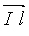 et et  sont colinéaires, le
force de LAPLACE vaut sont colinéaires, le
force de LAPLACE vaut 
REMARQUE 2 : voici un procédé mnémotechnique pour appliquer :
la
règle des 3 doigts de la main droite :
En
courant dans les champs, on prend les forces m
 pouce pouce  Index Index 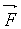 majeur majeur
|

![]() :
:




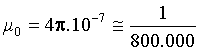 )
)